Cùng tìm hiểu về mã hoá đường cong Elliptic cơ bản và cách ứng dụng chúng trong trao đổi khoá Diffie-Hellman qua bài viết dưới đây. Để hiểu được bài viết này, người đọc cần biết đến một số kiến thức cơ bản về hai phần sau đây:
- Lý thuyết đại số cơ bản về nhóm, vành, trường
- Lý thuyết về hệ mật mã khoá công khai.
Mở đầu
Thuật toán mã hoá bất đối xứng dựa trên các bài toán khó có độ khó logarit rời rạc, ví dụ như thuật toán mã hoá RSA, hệ mật mã ElGammal, v.v.
Trong bài viết này, chúng ta sẽ nói đến một bài toán khó khác cũng được ứng dụng trong các thuật toán mã hoá bất đối xứng: mã hoá đường cong Elliptic trong trường hữu hạn số nguyên tố.
Cơ sở toán học
Về cơ bản, đường cong Elliptic trong trường hữu hạn số nguyên tố được định nghĩa như sau:
Cho p là số nguyên tố bất kỳ \(p>3\). Một đường cong \(E\) được định nghĩa trên \(F_p\) có phương trình (1):
$$y^2 = x^3 + Ax + b$$
trong đó: \(A, B ∈ Fp\), \(4a3 + 27b2 \ne 0\). Ta viết \(E/F_p\) biểu thị rằng \(E\) được xách định trong trường \(F_p\)
Điều kiện \(4a3 + 27b2 \ne 0\) đảm bảo rằng phương trình không có nghiệm kép. Điều này để tránh một số tình huống đặc biệt.
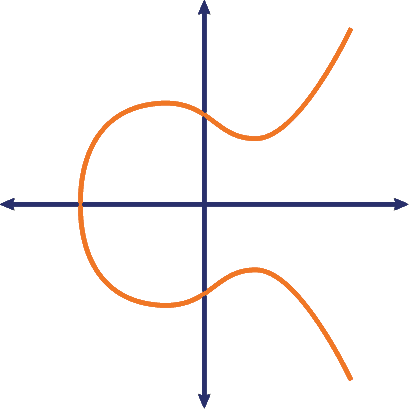
- Tập hợp các điểm trên đường cong:
- Cho \(E/F_p\) là một đường cong elliptic, và \(e > 1\). Chúng ta nói rằng một điểm \(x_1, y_1\) là một điểm trên đường cong \(E\) nếu \(x_1, y_1\) thoả mãn phương trình (1).
- Đường cong sẽ có một điểm đặc biệt \(O\) gọi là điểm vô cực. Mục đích của điểm này sẽ được nhắc đến sau. Chúng ta viết \(E(F_p)\) để chỉ tập hợp tất cả các điểm trên đường cong $E$ xác định trên \(F_p\), bao gồm cả điểm \(O\).
- Ví dụ: Xét đường cong \(E\) : \(y^2 = x^3+1\) trên trường \(F_{11}\). Khi đó:
$$E(F_{11}) = {O,\ (-1,0),\ (0,± 1),\ (2,±3),\ (5,±4), \ (7,±5),\ (9,±2)\ }$$
- Đường cong này có 12 điểm trên \(F_{11}\), ta viết rằng \(|E(F_{11})|=12\)
- Phép tính cộng trên đường cong Elliptic
- Trước hết, ta định nghĩa điểm vô cực \(O\) là phần tử đồng nhất, tức là, với mọi \(P ∈ E(F_p)\), ta định nghĩa \(P + O = O+P=P\)
- Bây giờ, cho \(P=(x_1,y_1)\) và \(Q=(x_2,y_2)\) là 2 điểm trên \(E(F_p)\). Tổng \(P+Q=(x_3,y_3)\) là được được xác định bằng một trong ba quy tắc sau:
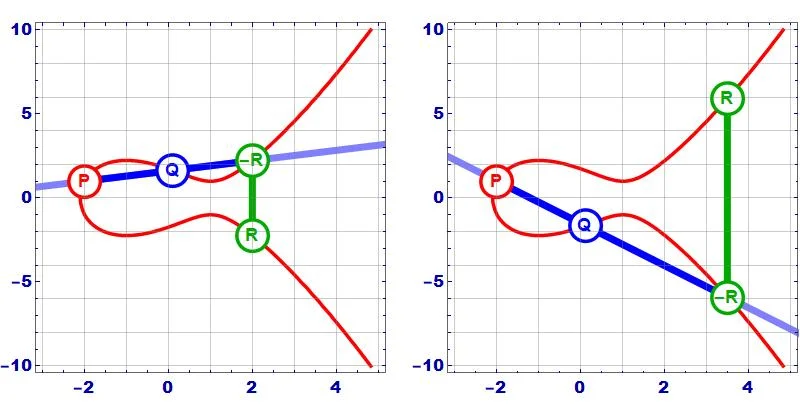
- Nếu \(x_1 \ne x_2\), nối 2 điểm \(P\), \(Q\) cắt đường cong tại 1 điểm gọi là \(-R\). Lấy đối xứng của \(-R\) qua trục \(Ox\) ta được điểm \(R = P+Q\). Cách tính toạ độ \(x_3,y_3)\):
- Đặt \(s_c := \frac{y_1-y_2}{x_1-x_2}\), khi đó
- \(x_3 := s_c^2 -x_1-x_2\)
- \(y_3 := s_c(x_1-x_3)-y_1\)
- Nếu \(x_1 \ne x_2\), nối 2 điểm \(P\), \(Q\) cắt đường cong tại 1 điểm gọi là \(-R\). Lấy đối xứng của \(-R\) qua trục \(Ox\) ta được điểm \(R = P+Q\). Cách tính toạ độ \(x_3,y_3)\):
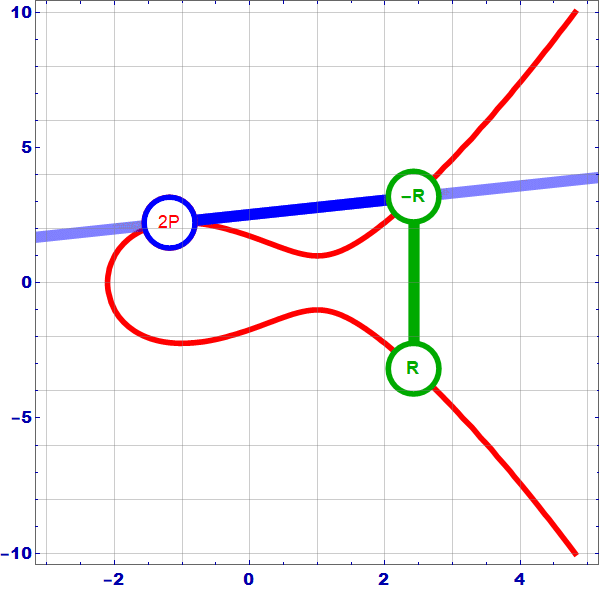
- Nếu \(x_1=x_2\) và \(y_1=y_2\ne 0\) (tức là \(P=Q\)). Khi đó ta kẻ tiếp tuyến của đường cong tại điểm \(P\) cắt đường cong tại điểm \(-R\). Lấy đối xứng của \(-R\) qua trục \(Ox\) ta được điểm \(R = P+P=2P\). Cách tính toạ độ \(x_3,y_3)\)
- Đặt \(s_t\):=\(frac{3x_1^2+a}{2y_1}\), khi đó
- \(x_3 := s_t^2-2x_1\)
- \(y_3:=s_t(x_1-x_3)-y_1$\)
- Nếu $x_1 = x_2$ và $y_1 = -y_2$, ta sẽ coi $P + Q = O$
- Phép cộng này biến tập hợp \(E(F_p)\) thành một nhóm. Phần tử đơn vị là điểm vô cực \(O\). Mọi điểm khác điểm vô cực \(O \ne P = (x_1, y_1) ∈ E(F_p)\) đều có nghịch đảo cộng, cụ thể \(-P = (x_1, -y_1)\). Có thể chứng minh rằng phép cộng này có tính chất kết hợp. Phép cộng này cũng có tính giao hoán, tức là \(P + Q = Q + P\) với mọi \(P, Q ∈ E(F_p)\). Dẫn đến nhóm này là nhóm abel.
- Giống như mọi nhóm, với một điểm \(P ∈ E(F_p)\), ta viết \(2P := P + P\), \(3P := P+P+P\) và \(alpha P := (\alpha - 1)P + P\) với mọi số nguyên dương \(alpha\). Lưu ý: \(alpha P\) có thể được tính bằng không quá \(2 \log_2\alpha\) phép toán bằng phương pháp lặp.
Áp dụng đường cong Elliptic trong trao đổi khoá Diffie-Hellman
ECDH (Elliptic Curve Diffie–Hellman Key Exchange) là một phương thức thỏa thuận khóa ẩn danh, cho phép hai bên, mỗi bên có một cặp khóa công khai - khóa bí mật trên đường cong elliptic, thiết lập một bí mật chia sẻ qua một kênh không an toàn. ECDH rất giống với thuật toán DHKE (Diffie–Hellman Key Exchange) cổ điển, nhưng nó sử dụng phép nhân điểm ECC thay vì phép mũ modulo. ECDH dựa trên tính chất sau của các điểm trong đường cong Elliptic:
$$ (a * G) * b = (b *G) *a $$
Nếu chúng ta có hai số bí mật a và b (hai khóa bí mật, thuộc về Alice và Bob) và một đường cong elliptic ECC với điểm sinh G, chúng ta có thể trao đổi qua một kênh không an toàn các giá trị \(aG)\) và \(bG)\) (các khóa công khai của Alice và Bob) và sau đó chúng ta có thể tạo ra một bí mật chia sẻ: \(secret = (a * G) * b = (b * G) * a\)
Tổng quát hoá phương trình trên sẽ là:
$$ AlicePubKey \ * BobPrivKey\ = BobPubKey\ * AlicePrivKey\ = SharedKey $$
Thuật toán ECDH sẽ như sau:
- Alice tạo một cặp khoá ECC ngẫu nhiên: \(\{AlicePrivKey, AlicePubKey = AlicePrivKey * G\}\)
- Bob tạo một cặp khoá ECC ngẫu nhiên: \(\{BobPrivKey, BobPubKey = BobPrivKey * G\}\)
- Alice và Bob trao đổi khoá công khai của họ thông qua một kênh không an toàn
- Alice tính \(sharedKey = BobPubKey * AlicePrivKey\)
- Bob tính \(sharedKey = AlicePubKey * BobPrivKey\)
- Giờ Alice và Bob có thể sử dụng $shareKey$ để mã hoá và trao đổi thông tin với nhau trên các kênh không an toàn
Tổng kết
Phần lớn của mật mã hiện đại dựa trên trao đổi Diffie-Hellman, yêu cầu hai bên mã hoá tin nhắn của họ với một bí mật chung mà các kẻ nghe lén không thể tìm ra được.
Elliptic-curve Diffie-Hellman cho phép hai bên thiết lập một khoá bí mật chung dựa trên lý thuyết về đường cong Elliptic.
Bài viết tiếp theo sẽ hướng dẫn sử dụng thư viện sagemath để tính toán đối với đường cong Elliptic.
Tài liệu tham khảo
- Dan Boneh & Victor Shoup (2023), A Graduate Course in Applied Cryptography
- Mark Hughes (2019), How Elliptic Curve Cryptography Works






